TOWER OF HANOI

The Tower of Hanoi (also called the Tower of Brahma or Lucas’ Tower ) is a mathematical game or puzzle. It consists of three rods and a number of disks of different sizes, which can slide onto any rod. The puzzle starts with the disks in a neat stack in ascending order of size on one rod, the smallest at the top, thus making a conical shape.

The objective of the puzzle is to move the entire stack to another rod, obeying the following simple rules:

1.    Only one disk can be moved at a time.

2.    Each move consists of taking the upper disk from one of the stacks and placing it on top of another stack.

3.    No disk may be placed on top of a smaller disk.

 

                                  Tower of Hanoi

 

ORIGIN…..

The puzzle was invented by the French mathematician Édouard Lucas in 1883. Everything in the world of science or maths has some or the other link with INDIA. There is a story about an Indian temple in Kashi Vishwanath which contains a large room with three time-worn posts in it, surrounded by 64 golden disks. Brahmin priests, acting out the command of an ancient prophecy, have been moving these disks in accordance with the immutable rules of Brahma since that time. The puzzle is therefore also known as the Tower of Brahma puzzle. According to the legend, when the last move of the puzzle is completed, the world will end. It is not clear whether Lucas invented this legend or was inspired by it.

If the legend were true, and if the priests were able to move disks at a rate of one per second, using the smallest number of moves it would take them 2⁶⁴ − 1 seconds or roughly 585 billion years to finish, which is about 42 times the current age of the Universe.

There are many variations on this legend. For instance, in some tellings the temple is a monastery, and the priests are monks. The temple or monastery may be said to be in different parts of the world — including Hanoi, Vietnam, — and may be associated with any religion. In some versions other elements are introduced, such as the fact that the tower was created at the beginning of the world, or that the priests or monks may make only one move per day.

 SOLUTION…….

The puzzle can be played with any number of disks, although many toy versions have around 7 to 9 of them. The minimal number of moves required to solve a Tower of Hanoi puzzle is 2ⁿ − 1, where n is the number of disks.^] This is precisely the nth Mersenne number.

The minimal number of moves required to solve a Tower of Hanoi puzzle is 2ⁿ − 1, where n is the number of disks.

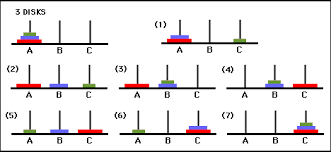
With 3 disks, the puzzle can be solved in 7 moves.

With 4 disks, the puzzle can be solved in 15 moves.

With 5 disks, the puzzle can be solved in 31 moves and so on….

 

           BY  USING RECURSION…..

 

The key to solving a problem recursively is to recognize that it can be broken down into a collection of smaller sub-problems, to each of which that same general solving procedure that we are seeking applies, and the total solution is then found in some simple way from those sub-problems’ solutions. Each of thus created sub-problems being “smaller” guarantees that the base case(s) will eventually be reached. Thence, for the Towers of Hanoi:

 

 

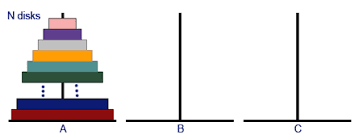
 label the pegs A, B, C,

·         let n be the total number of disks,

·         number the disks from 1 (smallest, topmost) to n (largest, bottom-most).

Assuming all n disks are distributed in valid arrangements among the pegs; assuming there are m top disks on a source peg, and all the rest of the disks are larger than m, so they can be safely ignored; to move m disks from a source peg to a target peg using a spare peg, without violating the rules:

1.     Move m – 1 disks from the source to the spare peg, by the same general solving procedure. Rules are not violated, by assumption. This leaves the disk m as a top disk on the source peg.

2.     Move the disk m from the source to the target peg, which is guaranteed to be a valid move, by the assumptions — a simple step.

3.     Move the m – 1 disks that we’ve just placed on the spare, from the spare to the target peg by the same general solving procedure, so they are placed on top of the disk m without violating the rules.

4.     The base case being to move 0 disks, that is, do nothing – which obviously doesn’t violate the rules.

 

The full Tower of Hanoi solution then consists of moving n disks from the source peg A to the target peg C, using B as the spare peg.

                                     RECURSION CODE….

// C recursive function to solve tower of hanoi puzzle

void towerOfHanoi(int n, char from_rod, char to_rod, char aux_rod)

{

 if (n == 1)

         {

        printf(“n Move disk 1 from rod %c to rod %c”, from_rod, to_rod);

          return;

          }

    towerOfHanoi(n-1, from_rod, aux_rod, to_rod);

    printf(“n Move disk %d from rod %c to rod %c”, n, from_rod, to_rod);

    towerOfHanoi(n-1, aux_rod, to_rod, from_rod);

}

The above code is a snippet  in the entire code we just need to pass the number of  disks in a tower and names which we want to give to the towers. In the above explanation I assumed it to be A,B,C.

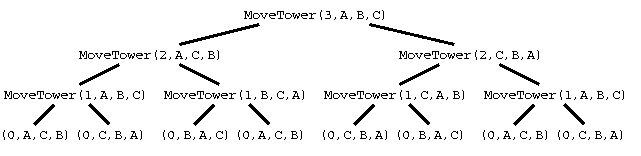
Another way to visualize what happens when you run MoveTower is called a call tree. This is a graphic representation of all the calls. Here is a call tree for MoveTower(3,A,B,C).

            

 

OUTPUT…

 

Input : 2

Output : Disk 1 moved from A to B

         Disk 2 moved from A to C

         Disk 1 moved from B to C

 

Input : 3

Output : Disk 1 moved from A to C

         Disk 2 moved from A to B

         Disk 1 moved from C to B

         Disk 3 moved from A to C

         Disk 1 moved from B to A

         Disk 2 moved from B to C

         Disk 1 moved from A to C

 

https://www.cs.cmu.edu/~cburch/survey/recurse/hanoiimpl.html

https://www.cs.cmu.edu/~cburch/survey/recurse/hanoiex.html

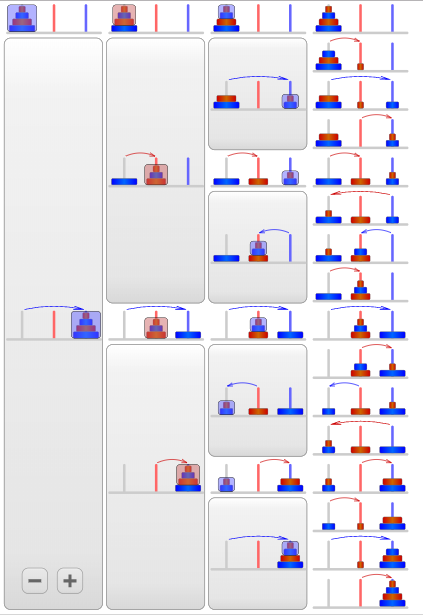
following these links will lead to a step by step tracing of tower of Hanoi solution recursively from where we can completely understand the recursions taking place at background.

The call stack in the display above represents where we are in the recursion. It keeps track of the different levels going on. The current level is at the bottom in the display. When we make a new recursive call, we add a new level to the call stack representing this recursive call. When we finish with the current level, we remove it from the call stack (this is called popping the stack) and continue with where we left off in the level that is now current.

I hope this link and the explanation proves useful to you…

Thanks for reading..

ADITYA KUMAR

1CR16IS007